Hình chóp tam giác đều là một dạng hình học không gian quan trọng trong chương trình Toán 8. Bài viết này sẽ cung cấp kiến thức tổng quan về hình chóp tam giác đều, bao gồm định nghĩa, công thức tính diện tích xung quanh, thể tích và các dạng bài tập thường gặp. Hi vọng bài viết sẽ giúp các em học sinh nắm vững kiến thức và vận dụng hiệu quả vào việc giải bài tập.
Khái Niệm Hình Chóp Tam Giác Đều
Hình chóp tam giác đều là hình chóp có đáy là một tam giác đều và các mặt bên là các tam giác cân bằng nhau có chung đỉnh.
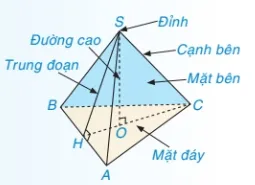 Hình chóp tam giác đều
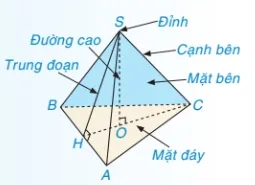
Hình chóp tam giác đều
- Đỉnh: Đỉnh chung của các tam giác cân.
- Cạnh bên: Các cạnh của tam giác cân (không phải cạnh đáy).
- Mặt bên: Các tam giác cân.
- Mặt đáy: Tam giác đều.
- Đường cao: Đoạn thẳng nối từ đỉnh đến trọng tâm của tam giác đáy.
- Trung đoạn: Đường cao của mỗi mặt bên.
Diện Tích Xung Quanh và Thể Tích Hình Chóp Tam Giác Đều
Diện tích Xung Quanh
Diện tích xung quanh của hình chóp tam giác đều được tính bằng tích của nửa chu vi đáy và trung đoạn.
Công thức: Sxq = p.d
Trong đó:
- p: nửa chu vi đáy
- d: trung đoạn
Thể Tích
Thể tích của hình chóp tam giác đều được tính bằng 1/3 tích của diện tích đáy và chiều cao.
Công thức: V = (1/3)S.h
Trong đó:
- S: diện tích đáy
- h: chiều cao
Bài Tập Hình Chóp Tam Giác Đều Toán 8
Dưới đây là một số bài tập về hình chóp tam giác đều theo các bộ sách giáo khoa khác nhau:
Bài Tập Kết Nối Tri Thức
Bài 10.1: Xác định đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao và trung đoạn của hình chóp.
Bài 10.3: Cho hình chóp tam giác đều S.MNP. Tính diện tích đáy và thể tích hình chóp.
Bài Tập Chân Trời Sáng Tạo
Bài 1 & 2: Xác định các mặt bên, mặt đáy và độ dài các cạnh của hình chóp tứ giác đều và tam giác đều.
Bài Tập Cánh Diều
Bài 1: Xác định miếng bìa nào có thể gấp thành hình chóp tam giác đều.
Bài 2 & 3: Tính diện tích xung quanh và thể tích của hình chóp tam giác đều.
Kết Luận
Bài viết đã tổng hợp kiến thức cơ bản về hình chóp tam giác đều toán 8, bao gồm định nghĩa, công thức tính diện tích, thể tích và một số bài tập minh họa. Hy vọng bài viết này sẽ hữu ích cho các em học sinh trong quá trình học tập và ôn luyện môn Toán. Để tìm hiểu thêm về các kiến thức Toán 8 khác, các em có thể tham khảo các bài viết liên quan được đề cập ở cuối bài gốc.